- Analytical methods to simplify/solve systems of partial differential equations(PDEs) These involve
- Reducing the system to first order by introducing new variables
- Reducing the system to locally solvable form by adding to it all first order PDEs obtainable by combining all the first derivatives of the PDEs with respect to each independent variable
- Look for linear combinations of the system that are expressible in fewer dimensions (i.e. number of independent variables)
- solve these explicitly if possible and subtitiute the solution back into the system so reducing the number of unknowns by 1(depends on knowing boundary conditions)
- Methods for solving equations involving an unknown function of a complex variable. For example
solve
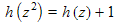 for the function
for the function 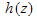 . These methods use the idea that analytic functions are
characterised by their behaviour at singular points and their topological properties about such points e.g. the winding number ratio (e.g.
. These methods use the idea that analytic functions are
characterised by their behaviour at singular points and their topological properties about such points e.g. the winding number ratio (e.g. 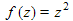 has singular point at z=0 with winding number ratio 1:2 there,
has singular point at z=0 with winding number ratio 1:2 there, 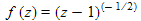 has a singular point z=1 winding number ratio -2:1 there), when considered as mappings defined over the entire complex plane including the point at infinity. Singular points
has a singular point z=1 winding number ratio -2:1 there), when considered as mappings defined over the entire complex plane including the point at infinity. Singular points 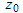 in the solution of an equation occur where z is such that an inconsistency arises such that no finite value of
in the solution of an equation occur where z is such that an inconsistency arises such that no finite value of 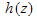 can solve the problem, in this example at z=0 or 1. Similarly singular points occur when the function
can solve the problem, in this example at z=0 or 1. Similarly singular points occur when the function 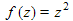 applied repeatedly gives 0 or 1. Such points are dense on the unit circle and 0. By considering the asymptotic behaviour of h(z) near 1:
applied repeatedly gives 0 or 1. Such points are dense on the unit circle and 0. By considering the asymptotic behaviour of h(z) near 1: 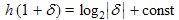 and a similar result holds round the unit circle. By considering analytic functions having this property
and a similar result holds round the unit circle. By considering analytic functions having this property  solves the equation.
A similar method shows that
solves the equation.
A similar method shows that  has solution
has solution  formally, but there is a problem with the multivalued nature of the ln function that affects the denominator. The same effect in the numerator gives a constant that can be combined with the arbitrary additive constant.
formally, but there is a problem with the multivalued nature of the ln function that affects the denominator. The same effect in the numerator gives a constant that can be combined with the arbitrary additive constant.
- Simplification of sets of polynomial equations by a generalisation
of the Euclidean algorithm
pdf(90kb)
LaTeX(12kb) This is likely to be equivalent to construction of Groebner bases.
- Related to the above, the development of algorithms that can be used by computer algebra systems (e.g. YACAS)
Equations done with the help of mathcast
Home
 for the function
for the function 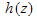 . These methods use the idea that analytic functions are
characterised by their behaviour at singular points and their topological properties about such points e.g. the winding number ratio (e.g.
. These methods use the idea that analytic functions are
characterised by their behaviour at singular points and their topological properties about such points e.g. the winding number ratio (e.g. 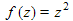 has singular point at z=0 with winding number ratio 1:2 there,
has singular point at z=0 with winding number ratio 1:2 there, 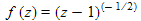 has a singular point z=1 winding number ratio -2:1 there), when considered as mappings defined over the entire complex plane including the point at infinity. Singular points
has a singular point z=1 winding number ratio -2:1 there), when considered as mappings defined over the entire complex plane including the point at infinity. Singular points 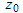 in the solution of an equation occur where z is such that an inconsistency arises such that no finite value of
in the solution of an equation occur where z is such that an inconsistency arises such that no finite value of 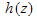 can solve the problem, in this example at z=0 or 1. Similarly singular points occur when the function
can solve the problem, in this example at z=0 or 1. Similarly singular points occur when the function 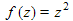 applied repeatedly gives 0 or 1. Such points are dense on the unit circle and 0. By considering the asymptotic behaviour of h(z) near 1:
applied repeatedly gives 0 or 1. Such points are dense on the unit circle and 0. By considering the asymptotic behaviour of h(z) near 1: 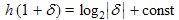 and a similar result holds round the unit circle. By considering analytic functions having this property
and a similar result holds round the unit circle. By considering analytic functions having this property 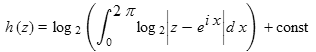 solves the equation.
A similar method shows that
solves the equation.
A similar method shows that 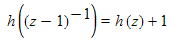 has solution
has solution 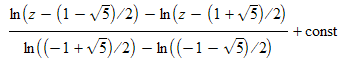 formally, but there is a problem with the multivalued nature of the ln function that affects the denominator. The same effect in the numerator gives a constant that can be combined with the arbitrary additive constant.
formally, but there is a problem with the multivalued nature of the ln function that affects the denominator. The same effect in the numerator gives a constant that can be combined with the arbitrary additive constant.